February 15, 2010 (Vol. 30, No. 4)
Maik W. Jornitz President and CEO G-CON Manufacturing
Theodore H. Meltzer Ph.D. founder Capitola Consulting
Examining the Order of Particle Removal by Filtration from Dilute Suspensions
In this article, we discuss a hypothetical filtration procedure in terms of particles, pores, and liquid flows with a view toward understanding how pores or interstices respond to given particulate challenges. We synthesized several experimental findings, regarding the challenging of filters—depth or membrane—with dilute suspensions.
This article will also differentiate between particle arrests caused by the (normally assumed) size exclusion or sieve retention mechanism, and those retained by the (usually ignored) adsorptive sequestration technique.
A comprehensive investigation of the removal of latex spheres from liquid suspensions by membrane filters has been performed by a group of experimentalists at the Particle Technology Laboratory of the University of Minnesota. Their findings have found practical application in semiconductor manufacturing. They are likewise relevant to the needs of pharmaceutical processing.
These investigations have employed particle suspensions in dilute aqueous systems in which surfactant molecules were ingredients. The particle concentrations, measured by particle counters, were approximately one-fifth those usually utilized in latex bead studies. One particular study by Lee et al. (1993), led to conclusions analyzed by Zeman that are a subject of discussion in this article.
Particle Size and Shape
The stage on which filtration takes place consists of an effective filtration area (EFA) marked by a pore size or retention distribution that is confronted by a particle size distribution. The particles consist of a range of sizes that are differentiated into two groups, each of which is defined by their size relative to the pore sizes.
One portion consists of the larger particles that are too big to fit through any of the distributed pores or fiber matrices, whether large or small. The other size particles are small enough to penetrate the larger pores or fiber interstices but not the smaller.
The pores or fiber interstices also constitute two size groups, only one of which covers a range of pore-size ratings large enough to be passed through by particles of the smaller sizes.
Depending upon the relative proportion of smaller and larger particles, and on the pore or interstice sizes they encounter, whether directed by the flow pattern or by chance, there will be different outcomes to the particle retentions, to the onset of filter plugging, and to the quantity of throughput.
This definition of particle sizes is a bit too neat to apply absolutely to any particle shapes except spheres directed toward circular pores. It begs an invariant sieving action based strictly on particle/pore sizes unaffected by shape factors. However, except for spheres, a particle’s longitudinal and transverse axes may differ in size. In a filtration, it is the particle’s dimensional axis that coincides with the pore that is the functional determinant of the particle’s size.
Probability factors, for example the particle’s axial orientations, governed by the liquid stream’s velocities, viscosities, and drag can result in a more-elongated needle–like shape, either passing through or lying athwart a pore opening. Thus, in a mixture of particles characterized generally as being too large to permeate a pore or fiber matrix interstice, some particles of particular shapes may do so depending upon how their flow pattern is directed by the filtration conditions or by chance.
Not surprisingly, in specific experimental trials, conclusions were reached that some particles of the group size seen as being too large to pass through the filter actually did so. This is not a contradiction of the sieving mechanism, but rather a more realistic description of size as defined by the particle dimensions that are limiting in any actual filtration. It might be simpler to refer to these membranes as being intermediate in size.
One is obliged to describe them as they are referred to in the literature, i.e., as larger particles. The implications are that they are too large to pass through the filter’s smaller pores. However, when properly aligned they can permeate a larger pore, bearing in mind that pore size labels are generally descriptive and the actual pore structure is typically larger than labeled.
Experimental Findings
Experiments by Lee et al. (1993-a) involved latex concentrations of 108 to 1010 per liter of one of each of five particle sizes, namely, 0.91 µm, 0.84 µm, 0.74 µm, 0.64 µm, and 0.45 µm, in aqueous suspensions containing 0.1% of a surfactant (Triton X-100) at a pH 7.1. Each individual suspension was used to exert a continuous challenge against a 0.45 µm rated hydrophylized PVDF membrane.
It is known that surfactant molecules interfere with the adsorption of latex beads. The nonpolar ends of the surfactant molecules undergo hydrophobic adsorptions with the nonpolar surfaces of the hydrocarbonaceous latex particles thereby enlarging, by their coatings, the sizes of the latex spheres. This results in an increase in the distance separating the particle surface from the surface of the filter.
The influence of this steric hindrance nullifies the adsorption of the particle to the filter. The result is the promotion of particle permeations of the filter by the smaller particulates that might otherwise have been retained by adsorption. This serves to make the worst-case conditions, those productive of particle passage, even more severe. Perhaps not surprisingly, Emory et al., found that the effects of various surfactant types, each with its own molecular features, differ in the degree of their influence on the retention of latex particles.
How latex beads of different diameters, e.g., 0.91 µm, 0.84 µm, 0.74 µm, 0.64 µm, and 0.45 µm, might penetrate an appropriate filter, e.g., a 0.45 µm-rated membrane, would depend upon the presence or absence of a surfactant and its unique molecular identity. Interestingly, in the usual situation where surfactant is absent, these five different lattices would not show a differentiation, because they would all be subject to adsorptive sequestrations (Figure 1).
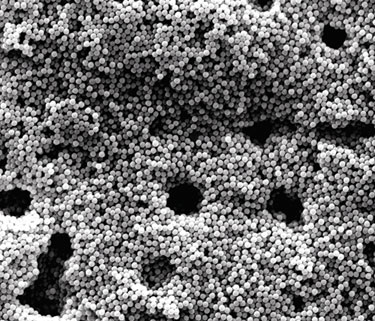
Figure 1. Latex beads adsorbed to a membrane surface
The analysis of the experimental data by Zeman is of particular interest. The log reduction values (LRV) obtained depended upon the particle loadings. Zeman refers to them as the number of pore volumes of removed particles (NPL). His analysis indicated that LRV levels decreased fourfold over the test’s duration. Plots of LRV against the number of pore volumes (NPV) removed by the filter, showed five different traces for five different latex-bead diameters (Figure 2). The LRVs showed a strong dependence on the particle loading.
In the usual situation where surfactant is absent, these five would not show a differentiation. This, in itself, is a benefit derived from working with dilute suspensions. According to Zeman, filter blockage occurred from the incipient cake formation when only 1% of the membrane pore volume (NPV, 0.01) was filled. With the larger particles, the greater build-up of filter cake caused the falling LRV to undergo an increase at higher NPVs.
The more numerous the particles and the larger their size, the more rapidly the filter’s porosity was blocked. The more rapid the blockage, the more restricted the throughput. From their work with latex beads, Emory et al., confirmed that “retention is strongly dependent on particle feed concentration.”
Zeman noted that the filters’ LRVs decreased some fourfold during the testing period. This translates to a fourfold increase in particle passage and was attributed to blockage of the smaller pores likely enhancing smaller particle flows to the larger pores with concomitant particle passage.
Zeman, in the context of surfactant being present, based his analysis of latex particle polydispersity upon the findings that when many larger particles were present, a reduction in the passage of smaller particles resulted. However, when the smaller particles were in greater numbers, more of the larger particles passed through the filter. Zeman reported that “the breakthrough of the smaller particles is retarded by the presence of larger particles,” and “the passage of larger particles occurs more rapidly when smaller particles are present in the stream.”
During filtration, fluid is simultaneously directed to both smaller and larger pores. According to the mean flow-pore concept, a small number of larger pores is seen to carry one-half the filter’s entire flow, while the remaining pores carry the other half. A far greater number of pores smaller than the mean flow pore are needed to balance the influence of the hydrodynamic preference for the larger pores. In line with the Hagen–Poiseuille equation, a greater proportion of smaller pores operating on the order of their radii to the fourth power serve to balance the greater flows of the larger pores.
With regard to particle retention, both larger and smaller particles would involve small pore blockage. The larger particles would similarly block larger pores. However, smaller particles could permeate larger pores. Blockage of the smaller pores will reduce their functional numbers, shifting the pore-size distribution in the direction of the larger pores. This will increase the likelihood of smaller particle penetrations in reverse proportion to the number of smaller pores still available.
In any case, to the extent that the proportion of larger particles dominates, their encounters with larger pores will exceed those of smaller particles. This will speed the closure of larger pores by larger particles. Nevertheless, until pore closure is complete, small particle passage can take place. This trend will continue until the larger pores are effectively blocked as judged by the rate of flow diminution.
In summation, the initial rate of particle passage will reflect the relative quantities of smaller and larger particles, and the numbers of smaller and larger pores, subject to mean flow-pore influences. As the smaller pores or interstices become increasingly blocked, whether by larger or smaller particles, the rate of smaller particle permeation in proportion to the number of larger pores will tend to increase, even as the number of larger pores is decreasing.
The rate of particle passage will progressively decrease as larger pores are successively blocked. The more numerous the larger particles, the faster the closure of pores through which the smaller particles can pass, and the less the overall number of filter penetrations. The earlier the termination of the filtration occurs, the lesser the amount of throughput.
Zeman’s second proposition, that “the passage of larger particles occurs more rapidly when smaller particles are present in the stream,” is also correct. Smaller particles block only the smaller pores of the filter. Due to the absence of adsorptive arrests, they have no effect on the progressive clogging of the larger pores leading eventually to their blocking. In effect, small particle competition with larger particles for occupying smaller pores, even if due only to their numbers, increases the frequency of larger particles coinciding with larger pores. To the extent that these larger particles are of shapes whose dimensions are suitably oriented within the flow stream to negotiate larger-pore passages, the presence of smaller particles enhances their filter penetrations.
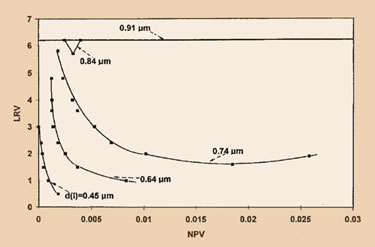
Figure 2. Log reduction values (LRV) over number of pore volumes (NPV)
Dilute Particle Suspension Effects
The liquid preparations utilized in this study were suspensions more dilute than are customarily employed. The investigations disclose insights not apparent from the experimental results garnered from more concentrated suspensions. Dilute suspensions represent worst-case situations, those least encouraging to particle retentions.
In more concentrated suspensions it is conceivable that so large a number of smaller particles may simultaneously arrive at a pore/fiber matrix as to give the appearance of its immediate blockage by a larger particle. This would result in a more rapid reduction in the number of larger pores, reducing over time the opportunities for smaller particles to penetrate them. It is a matter of the rate at which a sufficient mass of smaller particles reaches the larger pores to block them, and of the number of individual smaller particles that escape capture during the period of time leading up to the blockage.
The period during which the larger pores are available for penetration by the separate smaller particles of dilute suspensions is foreshortened in the case of concentrated dispositions, where more sudden pore blockages take place. Thus, the same total number of particles impacting a membrane over different durations can yield different throughputs. In essence, the diluter suspension represents the worst-case condition in that it makes more likely the escape of the smaller individual particles through still-unclogged larger pores.
As a result of the above discussion, it is posited that the coincidence of pores and particles can perhaps better be perceived when investigated in suspensions of dilute concentrations.
References
American Society for Testing and Materials (ASTM), ASTM Standard F-316-03 -2003. “Pore-Size Characteristics of Membrane Filters for Use with Aerospace Fluids,” ASTM, West Conshohocken, PA.
Emory S.F., Koga, Y., Azuma, N., Matsumoto, K. (1993). The Effects of Surfactant Type and Latex-Particle Feed Concentration on Membrane Retention, Ultrapure Water 10(2): 41–44.
Grant, D.C. and Zahka, J.G. (1990). Sieving Capture of Particles by Microporous Membrane Filters from Clean Liquids. Swiss Contamination Control 3(4a): 160–164.
Lee J.K., Liu B.Y.H., Rubow K.L. (1993-a). Latex Sphere Retention by Microporous Membranes in Liquid Filtration. J. Inst. Environ. Sci. 36(1): 26–36. (Jan./Feb).
Lee J., Liu B.Y.H., Rubow K.L. (1993-b) Latex Sphere Retention by Microporous Membranes in Liquid Filtration. J. Inst. Environ. Sci. 36(1): 26–36.
Lee, K. W., and Liu, B. Y. H. (1980). On the Minimum Efficiency and the Most Penetrating Particle Size for Fibrous Filters. Air Poll. Control Assoc. J. 30, 377–381.
Lee, J.K., Liu. B.Y.H., Rubow, K.L., and Zahka, J.G. (1990). Pore Size Characteristics of Microporous Membranes and Filters by Airflow Porosimetry and Particulate Loading Studies. Swiss Contamination Control. 3: 160–164.
Zahke, J.G. and Grant, D.C.(December 1991). Predicting the Performance Efficiency of Membrane Filters in Process Liquids Based on Their Pore-Size Ratings. Microcontaminants. pp. 23–29.
Zeman, L.J. (1996). Characterization of MF/UF Membranes. Chapter 4, pages 180–291 in Microfiltration and Ultrafiltration: Principles and Applications, Eds L.J. Zeman and A.L. Zydney, Marcel Dekker, New York, NY.
Maik W. Jornitz ([email protected]) is vp of product management FT/FRT at Sartorius Stedim North America. Web: www.sartorius-stedim.com. Theodore H. Meltzer, Ph.D. ([email protected]), is founder of Capitola Consulting.